Kait Lam supervised by Mark Utting, Ian Hayes, and Brae Webb
char[] a =
array bounds check elimination
↑
char[] b =
array bounds check elimination
for (int i = 0; i < a.length; i++) {
b[i] = a[i];
}
- Arrays are ubiquitous:
in C,char x[4]; in Java,char[] x. - In high level languages, compilers bounds-check every array access.
for (int i = 0; i < a.length; i++) {
assert 0 <= i < b.length;
assert 0 <= i < a.length;
b[i] = a[i];
}
- Arrays are ubiquitous:
in C,char x[4]; in Java,char[] x. - In high level languages, compilers bounds-check every array access.
- This makes things nice and safe — compilers must be safe.
- However, compilers have a competing goal of speed.
- Modern compilers support a plethora of optimisations.
- These are often intricate and prone to errors.
- [Yang 2011] found optimisations to be the most common source of compiler bugs.
| GCC | LLVM | |
|---|---|---|
| Front end | 0 | 10 |
| Middle end | 49 | 75 |
| Back end | 17 | 74 |
| Unclassified | 13 | 43 |
| Total | 79 | 202 |
formal methods
- This is a good case for formal verification!
- Each optimisation has an easily-defined specification:
- Analysis to find applicable optimisations.
- Transforms code in a predictable way (e.g. $x-x \mapsto 0$).
- The optimised code should behave identically to the original.
array bounds check elimination in GraalVM
with verification in Isabelle/HOL
background: the Graal compiler
- Graal is an optimising compiler for Java (and other languages).
- Features: just-in-time, ahead-of-time, native compilation.
- Supporting: Java, JavaScript, LLVM, Python, R, Ruby, WebAssembly, more...
- Optimisations must be fast with modest resource usage.
- Work in Graal might benefit any language which Graal can support.
background: the Graal IR
- Blends data-flow and control-flow into a single sea-of-nodes graph.
- Designed to simplify definition and application of optimisations.
- Also in static single-assignment form.
public static void f(int[] a, int[] b) {
for (int i = 0; i < a.length; i++) {
b[i] = a[i];
}
}
prior work: array bounds check elimination
- “ABCD: Eliminating Array Bounds Checks on Demand”
[Bodík et al. 2000] - Constructs an inequality graph from SSA.
- Redundancies found by shortest-path. Bodík et al. suggest a DFS.
- “Array bounds check elimination for the Java HotSpot™ client compiler” [Würthinger et al. 2007]
- Uses existing SSA CFG, traversed in dominator-first order.
- Fast but quite weak.
- “Eliminating partially-redundant array-bounds check in the Android Dalvik JIT compiler” [Absar & Shekhar 2011]
- Focuses on partially-redundant optimisations.
- Classifies variables into 'kinds' (loop index, invariant, dependent, ...).
background: verification in Isabelle/HOL
-
VeriOpt project led by Brae Webb, Mark Utting, Ian Hayes.
[Webb et al. 2021, Utting et al. 2023, Webb et al. 2023] - Existing definitions of Graal IR and Java values in Isabelle/HOL.
- Semantics for Graal IR.
- Framework for defining optimisations and verifying them.
- Validated with differential testing and Graal's unit tests.
- Existing work on verifying a flow-sensitive optimisation: conditional elimination.
LoadIndexedNode:
⟦ kind g nid = (LoadIndexedNode index guard array nid');
(* convert and evaluate the index *)
g ⊢ index ≃ indexE;
[m, p] ⊢ indexE ↦ indexVal;
(* convert and evaluate the array object *)
g ⊢ array ≃ arrayE;
[m, p] ⊢ arrayE ↦ ObjRef ref;
(* load from this index *)
h_load_field '''' ref h = arrayVal;
loaded = intval_load_index arrayVal indexVal;
(* record the result under this node id *)
m' = m(nid := loaded) ⟧
⟹ g, p ⊢ (nid, m, h) → (nid', m', h)
progress: tests and infrastructure
- A system of unit tests for testing effectiveness.
- Variations in: redundancy, index complexity, loop complexity, transitivity.
public class ArrayBoundsCheckEliminationTestCases {
public static int constant_p(int[] a) {
return a[5];
}
public static int constant_f(int[] a) {
if (!(0 <= 5 && 5 < a.length))
return -1;
return a[5];
}
public static int param_p(int[] a, int x) {
return a[x];
}
public static int param_f(int[] a, int x) {
if (!(0 <= x && x < a.length))
return -1;
return a[x];
}
public static int param_f_trans(int[] a, int x, int lower, int upper) {
if (!(0 <= lower))
return -1;
if (!(upper < a.length))
return -1;
if (!(lower <= x))
return -1;
if (!(x <= upper))
return -1;
return a[x];
}
public static int loop1_p(int[] a, int max) {
int s = 0;
for (int i = 0; i < max; i++) {
s += a[i];
}
return s;
}
public static int loop1_f(int[] a) {
int s = 0;
for (int i = 0; i < a.length; i++) {
s += a[i];
}
return s;
}
public static int loop1plus5_p(int[] a, int max) {
int s = 0;
for (int i = 0; i < max - 5; i++) {
s += a[i + 5];
}
return s;
}
public static int loop1plus5_f(int[] a) {
int s = 0;
for (int i = 0; i < a.length - 5; i++) {
s += a[i + 5];
}
return s;
}
public static int loop1plusc_p(int[] a, int max, int c) {
int s = 0;
for (int i = 0; i < max - c; i++) {
s += a[i + c];
}
return s;
}
public static int loop1plusc_f(int[] a, int c) {
int s = 0;
for (int i = 0; i < a.length - c; i++) {
s += a[i + c];
}
return s;
}
public static int loop1double_p(int[] a, int max) {
int s = 0;
for (int i = 0; i < max / 2; i++) {
s += a[2*i] + a[2*i+1];
}
return s;
}
public static int loop1double_f(int[] a, int c) {
int s = 0;
for (int i = 0; i < a.length / 2; i++) {
s += a[2*i] + a[2*i+1];
}
return s;
}
public static int loop2i_p(int[] a, int imax, int jmax) {
int s = 0;
for (int i = 0; i < imax; i++) {
for (int j = 0; j < jmax; j++) {
s += a[i];
s += a[j];
}
}
return s;
}
public static int loop2i_f(int[] a) {
int s = 0;
for (int i = 0; i < a.length; i++) {
for (int j = 0; j < a.length; j++) {
s += a[i];
s += a[j];
}
}
return s;
}
public static int loop2triangular_p(int[] a, int imax, int jmax) {
int s = 0;
for (int i = 0; i < imax; i++) {
for (int j = 0; j < i; j++) {
s += a[i];
s += a[j];
}
}
return s;
}
public static int loop2trianglular_f(int[] a) {
int s = 0;
for (int i = 0; i < a.length; i++) {
for (int j = 0; j < i; j++) {
s += a[i];
s += a[j];
}
}
return s;
}
public static int loop2lowertri_p(int[] a, int imax, int jmax) {
int s = 0;
for (int i = 0; i < imax; i++) {
for (int j = 0; j < i; j++) {
s += a[i];
s += a[j];
}
}
return s;
}
public static int loop2lowertri_f(int[] a) {
int s = 0;
for (int i = 0; i < a.length; i++) {
for (int j = 0; j < i; j++) {
s += a[i];
s += a[j];
}
}
return s;
}
public static int loop2uppertri_p(int[] a, int imax, int jmax) {
int s = 0;
for (int i = 0; i < imax; i++) {
for (int j = i; j < jmax; j++) {
s += a[i];
s += a[j];
}
}
return s;
}
public static int loop2uppertri_f(int[] a) {
int s = 0;
for (int i = 0; i < a.length; i++) {
for (int j = i; j < a.length; j++) {
s += a[i];
s += a[j];
}
}
return s;
}
public static int loop2sum_p(int[] a, int imax, int jmax) {
int s = 0;
for (int i = 0; i < imax; i++) {
for (int j = 0; j < jmax - i; j++) {
s += a[i + j];
}
}
return s;
}
public static int loop2sum_f(int[] a) {
int s = 0;
for (int i = 0; i < a.length; i++) {
for (int j = 0; j < a.length - i; j++) {
s += a[i + j];
}
}
return s;
}
public static int loop2sumplus5_p(int[] a, int imax, int jmax) {
int s = 0;
for (int i = 0; i < imax; i++) {
for (int j = 0; j < jmax - i - 5; j++) {
s += a[i + j + 5];
}
}
return s;
}
public static int loop2sumplus5_f(int[] a) {
int s = 0;
for (int i = 0; i < a.length; i++) {
for (int j = 0; j < a.length - i - 5; j++) {
s += a[i + j + 5];
}
}
return s;
}
public static int loop2addmul_p(int[] a, int imax, int jmax) {
int s = 0;
for (int i = 0; i < imax / 4; i++) {
for (int j = 0; j < 4; j++) {
s += a[j + 4 * i];
}
}
return s;
}
public static int loop2addmul_f(int[] a) {
int s = 0;
for (int i = 0; i < a.length / 4; i++) {
for (int j = 0; j < 4; j++) {
s += a[j + 4 * i];
}
}
return s;
}
}
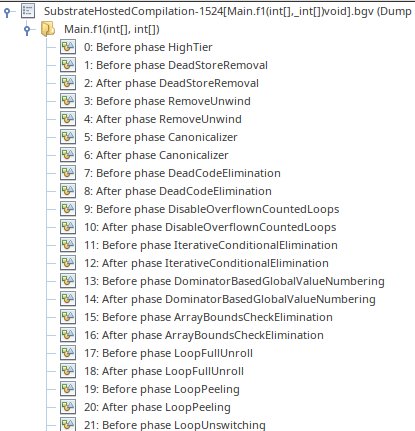
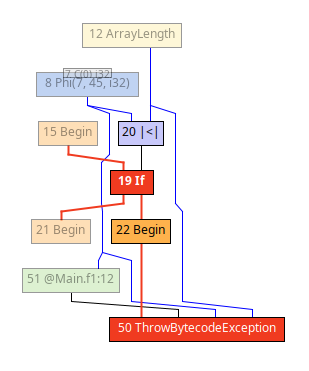
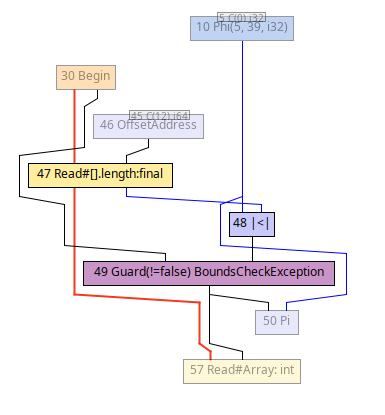
progress: tests and infrastructure
- modified Graal to emit graphs after each optimisation phase.
- variations between Graal's JIT mode and its native image compilation.
 |
 |
 |
 |
future work: implementation and verification
- bounds check elimination remains to be implemented.
- performance evaluation with benchmarks: SPECjvm2008, SciMark, ...
- verification.
questions?
Absar, J., & Shekhar, D. (2011). Eliminating partially-redundant array-bounds check in the Android Dalvik JIT compiler. Proceedings of the 9th International Conference on Principles and Practice of Programming in Java, 121–128. https://doi.org/10.1145/2093157.2093175
Bodík, R., Gupta, R., & Sarkar, V. (2000). ABCD: Eliminating array bounds checks on demand. ACM SIGPLAN Notices, 35(5), 321–333. https://doi.org/10.1145/358438.349342
Utting, M., Webb, B. J., & Hayes, I. J. (2023). Differential testing of a verification framework for compiler optimizations (case study). 2023 IEEE/ACM 11th International Conference on Formal Methods in Software Engineering (FormaliSE), 66–75. https://doi.org/10.1109/FormaliSE58978.2023.00015
Webb, B. J., Hayes, I. J., & Utting, M. (2023). Verifying term graph optimizations using Isabelle/HOL. Proceedings of the 12th ACM SIGPLAN International Conference on Certified Programs and Proofs, 320–333. https://doi.org/10.1145/3573105.3575673
Webb, B. J., Utting, M., & Hayes, I. J. (2021). A formal semantics of the GraalVM intermediate representation. In Z. Hou & V. Ganesh (Eds.), Automated Technology for Verification and Analysis (Vol. 12971, pp. 111–126). Springer International Publishing. https://doi.org/10.1007/978-3-030-88885-5_8
Würthinger, T., Wimmer, C., & Mössenböck, H. (2007). Array bounds check elimination for the Java HotSpotTM client compiler. Proceedings of the 5th International Symposium on Principles and Practice of Programming in Java - PPPJ ’07, 125. https://doi.org/10.1145/1294325.1294343
Yang, X., Chen, Y., Eide, E., & Regehr, J. (2011). Finding and understanding bugs in C compilers. ACM SIGPLAN Notices, 46(6), 283–294. https://doi.org/10.1145/1993316.1993532